Кинематика системы гонщик — велосипед

Кинематика системы в целом. Траектория движения системы гонщик — велосипед ограничена трассой — по­верхностью трекового полотна, шоссе или кроссовой до­роги. Во всех случаях, за исключением свободного полета (прыжков) при преодолении препятствий, движение велосипеда предполагает непрерывный контакт с поверх­ностью трассы. Именно этот контакт лежит в основе меха­ники движения велосипеда и его управления.

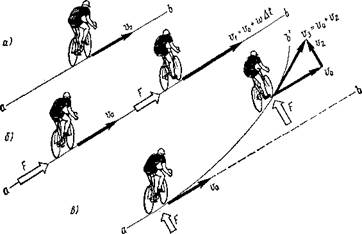
Рис. 8.3. Виды движения системы гонщик — велосипед

Согласно законам механики, изменения скорости и направления движения системы гонщик — велосипед не могут происходить без воздействия на нее внешних сил. При отсутствии последних система стремится сохранить состояние покоя или равномерного прямолинейного дви­жения. В этом случае вектор скорости системы и0 совпа­дает с направлением движения ab (рис. 8.3, а).

Для изменения скорости и направления движения системы необходима внешняя сила F, тем большая, чем больше масса системы т и ускорение w, которое ей тре­буется сообщить. Масса системы является мерой ее инерт­ности, т. е. способности сохранять неизменными пара­метры движения. Так, при воздействии внешней силы F со стороны дорожного покрытия в зоне контакта ведущего колеса с дорогой система получает ускорение w в течение
времени Дt и скорость движения становится равной юл = = у0 + wk. t (рис. 8.3, б).

Действие внешней силы способно изменить не только скорость, но и направление движения. Так, под действием силы F, направленной перпендикулярно к траектории движения, система приобретает дополнительную ско­рость v2. Суммарная скорость v3 = у0 + v2, будучи сум­мой двух векторов (рис. 8.3, в), является скоростью дви­жения системы по траектории ab’ в отличие от скорости у0

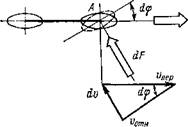
Рис. 8.4. Схема оценки условий, обе­спечивающих поворот велосипеда

прямолинейного движе­ния.

Итак, только нали­чие внешней силы по­зволяет осуществить по­ворот велосипеда, т. е. изменить первоначаль­ную траекторию дви­жения системы. Для анализа действия этой силы будем считать, что велогонщик, двигаясь прямолинейно со скоростью v (рис. 8.4), повернул руль в точке А на угол d(p. Пусть этот поворот осуществлен в момент времени t. Можно считать, что в момент времени t + dt переносная скорость системы упер в силу закона инерции практически не изменится ни по величине, ни по направлению. При повороте на угол d(p абсолютная ско­рость точки А контакта колеса с дорогой уже не равна нулю, так как переносная скорость оси упер и относи­тельная скорость у0тн точки А колеса не лежат на одной прямой. Скорость точки А становится равной dv и на­правлена в сторону угла поворота dtp.

Для изменения скорости движения на величину dv необходимо приложить внешнее усилие, которым может быть только сила трения колеса о поверхность дороги. Следовательно, при повороте колеса появляется сила трения dF, действующая на колесо в направлении dv, чем и обеспечивается необходимое ускорение системы. Очевидно, что при отсутствии сил трения или при недо­статочных их значениях контролируемый поворот стано­вится невозможным [4].

Практика показывает, что одновременно с поворотом необходимо осуществить наклон велосипеда в сторону центра кривизны, чтобы компенсировать центробежные силы инерции. Требуемый угол наклона tp приближенно можно определить из известного равенства

(8.1)

где і U. колеса

ctg|> = x?/(gR) < [(і I,

— допустимое значение коэффициента сцепления с дорожным покрытием; R — радиус кривизны

д) а

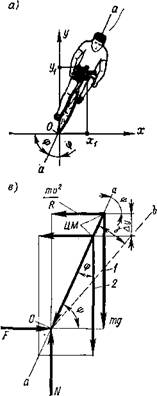
Рис. 8.5. Система гонщик — ве­лосипед при прохождении вира­жа: а — вариант 1; б — вариант 2; в — схема действующих сил;

1 — план сил для варианта 1; 2 «*■ план сил для варианта 2

виража; v — скорость движения; g — ускорение свобод­ного падения.

Это равенство получено на основании анализа сил, возникающих в системе гонщик — велосипед при про­хождении поворота с плоским дорожным покрытием (рис. 8.5). Ясно, что гонщик должен находиться верти-

кально, иначе он упадет. Но его вертикаль аа не совпа­дает с земной Оу, она наклонена под некоторым углом ср, который не зависит от массы т гонщика, а зависит от радиуса кривизны поворота и скорости его прохождения. Однако масса системы определяет величину силы реак — диии N дорожного полотна на колеса велосипеда и вели­чину силы трения F в зоне контакта колеса с дорогой. Устойчивость системы гонщик -— велосипед обеспечи­вается балансом моментов центробежной силы F ц = = mt?/R и гравитационной силы Fr = mg.

Для обеспечения предельной скорости прохождения виража, определяемой допустимым значением [fi], при­меняют прием смещения центра масс (ЦМ) системы в сто­рону, противоположную центру кривизны виража (рис. 8.5, б). Это позволяет сместить ЦМ вниз на величину &У — Уі — Уг> что, однако, не изменяет условий взаимо­действия системы с поверхностью дороги, определяемых углом 4% который образован линией аа, проходящей через точку опоры О и ЦМ системы, с горизонталью Ох. Допол­нительный угол наклона велосипеда у и вертикальное положение корпуса значительно повышают мобильность гонщика в управлении велосипедом и в достижении пре­дельных значений угла tp. Максимально возможные ско­рости прохождения виражей при различных покрытиях и состоянии дороги показаны на рис. 8.6.

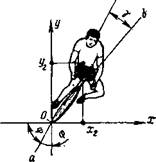
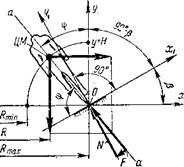
Аналогичный анализ может быть проведен и для усло­вий прохождения наклонных виражей велосипедного трека (рис. 8.7), где система координат хгОуг полотна трека развернута на угол (і относительно горизонта. В зависимости от скорости движения системы радиус кривизны R траектории движения ЦМ изменяется от Rmax при v = 0 до Rmln при v = утах. Уравнение (8.1) в дан­ном случае требует уточнения в связи с учетом радиуса кривизны траектории движения ЦМ системы гонщик — велосипед. В таком случае скорость прохождения виража в зависимости от угла <р выразится уравнением

V — Yg (Rmax — Н Sin ф) tg ф. (8.2)

Уравнение (8.2) приближенно описывает мгновенное значение скорости движения в данной точке виража. Общая картина изменения кинематических характери­стик системы при прохождении виражей значительно сложнее и зависит от целого ряда параметров: таких, как радиус кривизны виража, координаты его положений,

Рис. 8.6. Скорости прохождения виража с минимальным радиусом Rmi„ при различных покрытиях и состоянии дсроги: Кривая Иокрьп ие М. 1 Грави й сухой 0,4 0» 2 Асфальт мокрый 0,5 ud 3 » сухой 0,7 51 4 Бетон мокрый 0,8 17 5 » сухой 0,9 43

профиль виража, вид покрытия его поверхности, меха­нические характеристики системы гонщик — велосипед.

Приемы прохождения плоского виража существенно отличаются от приемов прохождения наклонного виража.

Плоский вираж — типовой вариант виража шоссей­ной трассы (рис. 8.8). Наиболее сложные условия про­хождения плоских виражей встречаются на спусках гор­ных участков трассы, где скорость движения может превышать 70 км/ч. Воз­можно бесчисленное мно­жество вариантов траек­торий прохождения пло­ского виража, из которых рассмотрим сначала две, имеющие общий центр

Рис.. 8.7. Схема действующих сил в системе гонщик — вело­сипед при прохождении на­клонного виража

кривизны О,: ABC (траекторию движения с радиусом Rt на расстоянии h от левого контура дорожного полотна шириной Н) и йнС„ (траекторию движения с радиусом R., на расстоянии h от правого контура дорожного полотна).

Прохождение виража по этим траекториям возможно в случае одновременного подхода к виражу двух гонщиков

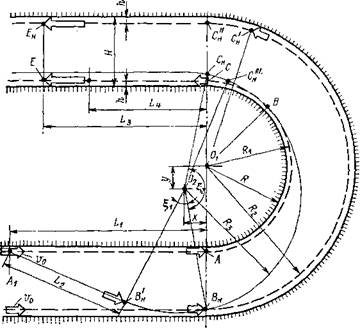
Рис. 8.8. Схема оценки кинематики прохождения велогонщиком пло­ского виража

соответственно в позициях А и 6Н. Согласно уравне­нию (8.1) гонщики должны снизить скорость входа в вираж от начального значения v0 до допустимых пределов: соот­ветственно vA и vBli. Так, при R = 15 м, Н = 8 м, h = = 0,5 м и сухом асфальтированном покрытии (ц = 0,4) максимальные скорости входа в вираж соответственно равны: для первого гонщика vA = 7,79 м/с (28 км/ч); для второго гонщика vbh = 9,39 м/с (33,8 км/ч). Несмотря на более высокую скорость прохождения по внешней траектории ВнСн проигрыш в расстоянии составит

СнСн = 11,92 м. Этот проигрыш будет ликвидирован только в точках Е и Е„ при тех же скоростях движения лишь через 7,44 с с момента выхода первого гонщика из виража в точке С, т. е. на расстоянии L3 = 58 м. При­веденный расчет показывает, что вариант прохождения виража по внешней траектории является проигрышным.

Рассмотрим дополнительный вариант траектории дви­жения АхВ’нВнВСн, которая описывается дугой окруж­ности радиуса R3 = 20,7 м. Центр кривизны 02 этой траектории смещен относительно центра Ох на расстоя­нии хну. Расчетная длина дуги ограничена углом 4- Ь.» Два сравниваемых гонщика движутся из одной точки At по рассматриваемой траектории и по траектории АгАВС. Можно считать, что путем предварительного торможения (тормозной путь первого гонщика Llt второго — L2 < < Lj) оба гонщика окажутся в исходных точках входа в вираж Л и SI, с предельно допустимыми скоростями движения: Va — 7,79 м/с (28 км/ч); vB■ — 9,01 м/с

(32 км/ч). Первый гонщик, идущий по внутренней траек­тории ABC, на выходе из виража в точке С окажется через 6,25 с. В это время второй гонщик, идущий по траектории В’ИВЯВСЯ, окажется в точке Сн, проигрывая первому гонщику в расстоянии СНСН = 8,72 м. Однако имея большую скорость на выходе из виража, второй гонщик догонит первого на расстоянии L4 — 55,68 м.

В реальных условиях прохождения плоского виража возможны и другие, более рациональные траектории дви­жения с переменными радиусами кривизны и режимами торможения, поиск и расчет которых достаточно сложны и в данном случае не рассматриваются.

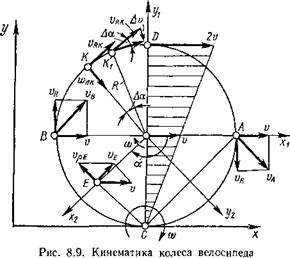
Кинематика колеса. Движение колеса имеет сложную структуру. Колесо перекатывается по поверхности дороги теоретически без проскальзывания, в то время как в дей­ствительности проскальзывание существует, но соста­вляет сравнительно небольшую величину.

Введем три системы координат (рис. 8.9): ху — непо­движную относительно поверхности дороги; хгуг — под­вижную и связанную с рамой велосипеда или осью колеса; хіУг — подвижную и связанную непосредственно с колесом, которая, таким образом, совершает сложное движение. Система координат хгуг совершает переносное поступа­тельное движение, в котором все точки имеют одинако­вую скорость v. Система координат х2у2 совершает отно­сительное вращательное движение, в котором каждая точка колеса движется с окружной скоростью ир = шр, где и — угловая скорость относительного движения; р — расстояние от начала координат 0Х до рассматривае­мой точки. Векторная сумма переносной и относительной скоростей любой точки колеса равна абсолютной [ско­рости: va = v + vp.

Точка С является точкой касания колеса с поверх­ностью дороги и является неподвижной при принятом выше условии — отсутствии проскальзывания колеса относительно дороги и деформации однотрубки. Ско­рость точки С, принадлежащей колесу (р = R), равна vc = v — vR — 0; следовательно, v = vR = mR. Угло­вая скорость вращательного движения ш = v/R. Ско­рость отдельных точек обода, например А, В, D, соста­вляет:

Уд — Vb ~ Vі — j — v% = v2; vD = V + vR = 2v.

Для произвольной точки Е колеса, находящейся на расстоянии р = 0lE от оси колеса, скорость определится как векторная сумма vE — v + vpE. Численное значение скорости точки Е может быть определено с помощью вы­ражения

vE — / tr — f — v-pE + 2vvpe cos a.

С другой стороны, плоскопараллельное движение колеса в каждый момент времени можно представить как вращение около мгновенного центра вращения. В данном случае мгновенным центром вращения является мгновен­ный центр скоростей в точке С, в котором скорость равна нулю. Положение мгновенного центра скоростей можно определить также как точку пересечения перпендикуля­ров к направлениям векторов абсолютных скоростей двух произвольных точек колеса, например А и Е.

Тогда скорость любой точки колеса определяется выражением v = сор, где со — угловая скорость вращения колеса вокруг мгновенного центра скоростей, равная угловой скорости вращения колеса вокруг своей оси Ох; р — расстояние от рассматриваемой точки до мгновен­ного центра вращения. Так, для точки D это расстояние составляет р0 = 2R, для точек А и В будет рв = рА = = RY2; для произвольной точки Е

р Е = ЕС = У Ре + R2 — 2р е R cos а.

Направлен вектор абсолютной скорости в сторону вращения перпендикулярно к соответствующему от­резку р, соединяющему мгновенный центр скоростей с рассматриваемой точкой.

Окружная скорость любой t’-й точки vRi направлена по касательной к траектории ее движения относительно оси вращения колеса Ot. По мере увеличения угла сс точка А последовательно занимает положения С, В и D, а вектор vRi, оставаясь постоянным по величине, меняет свое направление. Это объясняется наличием нормального ускорения движения даже при равномерном вращении колеса, т. е. при тангенциальном ускорении, равном нулю. При бесконечно малом угле поворота Да, на кото­рый колесо поворачивается за бесконечно малый отрезок времени At, скорости в точках /С и /Сх представляют собой равные по величине векторы vRK и vRKi, касательные к окружности в этих точках. Перенеся вектор скорости vRK в точку Ki, получим вектор Ду, представляющий собой изменение скорости точки К при переходе в положе­ние К за время At. Из подобия треугольников и с учетом того, что At -*■ 0, можно записать

Av — KKiVm/R — KKiVHKlR.

Отсюда следуег, что нормальное ускорение точки К

WnK = Vrk/R = Пі)2.

Это ускорение направлено к центру колеса и назы­вается центростремительным.

В случае неравномерного движения полное ускорение складывается из нормального и тангенциального, которые взаимно перпендикулярны: w — [(dv/dt)2 + u2IR))l/2.