Проблемы применения некруглых зубчатых звездочек в цепных передачах гоночных велосипедов

Велосипед, в частности гоночный, представляет собой уникальную по простоте конструктивного решения ма­шину, которая прошла испытание временем в условиях жесткой спортивной конкуренции. В настоящее время, когда проблема транспортных и пассажирских перевозок, можно сказать, практически решена, когда современный комфортабельный автомобиль стал доступен любому част­ному лицу, поток людей, пытающихся «изобрести» или по крайней мере усовершенствовать велосипед в целях наиболее эффективного использования его в быту, ни­сколько не убывает. Одним из центров внимания изобре­тателей является узел привода велосипеда. Их многочис­ленные попытки увеличить КПД системы привода тем не менее не дали однозначных положительных резуль­татов.

Практика использования велосипеда показала, что наиболее эффективной системой привода является цепной

привод с кривошипно-педальным механизмом. Признавая оптимальность этого конструктивного решения, изобре­татели и рационализаторы обратили внимание на цикличе­ский характер системы привода и на наличие так называе­мых мертвых зон при движении кривошипов в цикле педалирования, когда кривошипы находятся в вертикаль­ном положении. Эти зоны можно назвать мертвыми весьма условно, так как конструкция педалей, оснащенных тук — липсами, позволяет даже в мертвых зонах создавать кру­тящий момент на оси карет* ки гоночного велосипеда. Равенство крутящего мо­мента нулю или наличие отрицательного момента в этих зонах свидетельствует о низком качестве педали­рования, что недопустимо для гонщика даже низших спортивных разрядов.

торс кое решение привода гоноч­ного велосипеда с эллиптической передней звездочкой

Одновременно в цикле педалирования имеются наибо­лее активные зоны, когда кривошипы расположены гори­зонтально и создаются условия максимального приложе­ния усилий со стороны СНКГ. В этих условиях целесооб­разно иметь такую систему привода, которая автомати­чески изменяла бы передаточное отношение между криво­шипом и колесом с учетом положения кривошипа: когда кривошип приближается к горизонтальному положению, передаточное отношение плавно уменьшается, а когда к вертикальному — увеличивается, так как ii2 = z2/zi.

Известны многочисленные патенты, предлагающие реа­лизацию синхронного изменения передаточного отношения системы кривошипно-педального цепного привода.

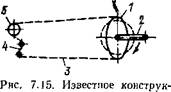
Наиболее удачное решение, дающее возможность ре­ально использовать эту идею, представлено на рис. 7.15. Решение предусматривает применение эллиптической звез­дочки установленной на оси каретки велосипеда, со­вместно с компенсатором изменения длины цепи в виде обычного суппера, применяемого на шоссейном гоночном велосипеде. Эллиптическая звездочка 1 развернута на

1 Идея использования эллиптических ведущих звездочек в при­воде велосипеда была известна еще в прошлом веке, когда одна из европейских фирм выпустила партию велосипедов с таким приводом, а американский гонщик Тейлор применял эллиптические звездочки в спринтерских гонках.

некоторый угол (в данном случае я/2) относительно кри­вошипа 2. Изменение длины цепи 3, вызванное изменением передаточного отношения от эллиптической звездочки 1 к звездочке 5 заднего колеса, компенсируется натяжной системой суппера 4.

Другое известное решение предусматривает примене­ние эксцентрично посаженных на кривошипы педалей. Ось педали установлена в кольце, смонтированном в обойме кривошипа, так, что при горизонтальном положении кри­вошипа его длина достигает наибольшего значения, на­пример 0,200 м, а при вертикальном положении — наи­меньшего, например 0,140 м. Французская фирма «Коль — ру», выпускающая велосипеды, оснащенные подобным приводом, гарантирует в рекламном проспекте снижение энергозатрат при педалировании на 12 % по сравнению с традиционным приводом. Кинематика этого конструк­тивного решения не ясна из опубликованных материалов фирмы, но сама идея решения интересна и может быть использована в реальных конструкциях гоночных вело­сипедов.

В первом и втором случаях решается задача изменения передаточного отношения по закону, определяемому эл­липсом передней звездочки цепного привода или эллип­сом, по которому изменяется длина кривошипа. Особен­ностью первого случая является непостоянство в цикле педалирования угла, заключенного между вертикалью и радиусом-вектором точки приема цепи на эллиптическую ведущую звездочку, особенностью второго случая — по­стоянство этого угла. Преимущество того или иного кон­структорского решения может быть оценено только с уче­том динамики процесса педалирования.

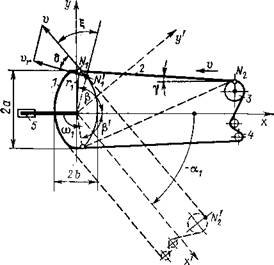
Привод с эллиптической ведущей звездочкой позволяет наиболее просто решить задачу синхронного изменения передаточного отношения при неизменных остальных де­талях механизма. Сложность проблемы состоит в том, чтобы установить, насколько целесообразно применять такой вид передачи вообще, и в том, чтобы в случае поло­жительного ответа на этот вопрос определить оптимальное соотношение полуосей эллиптической звездочки и угол сдвига осей звездочки относительно кривошипа. На рис. 7.16 представлена схема цепного привода гоночного велосипеда с эллиптической ведущей звездочкой. Цепь 2, сходящая в точке N2 с ведомой звездочки 3 в направлении стрелки v, набегает на ведущую эллиптическую звез­дочку / в точке с радиусом-вектором гг. Эффективным радиусом ведущей звездочки, определяющим действитель­ное передаточное отношение цепной передачи, будет ра­диус гг, являющийся функцией угла поворота криво­шипа аг. Излишек (недостаток) цепи компенсирует суп — пер 4. Кривошип 5 в данном случае совпадает с малой осью эллиптической ведущей звездочки.

Рис. 7.16. Схема цепного привода с эллиптической ведущей звездочкой

Задача анализа сводится к определению закономер­ности изменения угловой скорости вращения кривошипа при постоянной скорости схода цепи с ведомой звездочки в условиях равномерного движения велосипеда.

Для того чтобы оценить эффективность применения эллиптических ведущих звездочек в цепном приводе, рас­смотрим его конструктивную схему, в которой ведущая звездочка имеет изменяющиеся оси 2а и 2b (рис. 7.16), причем 0,5г0 -< b -< г0, где г0 — радиус окружности экви­валентной звездочки. Условие эквивалентности состоит в постоянстве среднеинтегрального значения передаточ­ного отношения цепной передачи за один оборот криво­шипа, т. е. длина делительной окружности круглой звез­дочки L„ = 2лг0 равна длине делительного контура эллип­
тической звездочки L6 т я [3/2 (a — f b) — улай]. Зада­ваясь малой осью эллипса 2b в указанном интервале, можно получить большую ось 2а:

а = (—В Вг — 9Л )/2,25, (7.36)

где

А = (2/3& — 2/-0)2; В = 7/2Ь — 6г0.

Ведущая ветвь цепи на участке NtN2 в первом при­ближении может быть рассмотрена в качестве прямой, касательной к эллипсу и проходящей через неподвижную точку N2 (хг, у2). Используя уравнение эллипса

х = b cos Р; у — a sin fi, (7.37)

уравнение касательной

x2xjb2 + УіУІсі1 = 1 (7.38)

cti; 1 (7.39) :os ai, J ‘

и выражения для координат точки No_ в подвижной си­стеме х’Оху’ при повороте этой системы в обращенном движении на угол —ах

*2 = *2 cos аі — у2 sin

г/2 = —*2 sin аі -{- 1/2 cos <

получим

Тогда выражения для определения угла |3 имеют вид: (7.40)

-Т — cos р + sin 0 = 1.

. о ab’y.-, ± ах.: Vcfixk Ь’гуп — а-£>-

Sin В = ——- ^——— — „ ,, , • . у:; ‘———-

г а? хгг + b2yl

„ a-bx, Т Ьи.-, ІҐaLx% 4- b-ui — a-b1

COS P = —— =—— о I ————

r a-xk + b-yi2

Верхний знак перед корнем в выражениях (7.40) соот­ветствует верхней касательной и углу |3, нижний — ниж­

ней касательной и углу f}’. Нас интересует только верхняя касательная, совпадающая с ведущей ветвью цепи.

Угол р лучше определять по синусу, так как он может находиться в первом или четвертом квадрантах.

Определим учитываемые в расчете углы у, £ и 6. Согласно уравнениям (7.37), проекции точки касания N{ на оси координат неподвижной системы хОху имеют вид:

/і Sin аь ) (7.41) /I cos а,. )

Xi = х cos ai — у і

у = х sin а, + у

Тогда

t&Y = Jr~- = T-> Y = arctg T-

(7.42)

x2 X

l = n — (Y + P + av); 6 = Y + p + a! — л/2.

Мгновенные значения кинематических параметров точ­ки ведущей ветви цепи, движущейся со скоростью v = const, определяются окружной скоростью vr, угло­выми скоростью (Oi и ускорением єх;

(7.43)

vT = v sin (ax 4- p 4- y); Ml = Vr/Гг’,

da і

Єі = 1ЕГ Wl = (dVr■’Tx ~ ^~7f

Здесь

dvr = t> cos (at 4- p + y) 0 4- 4- ^Y)>’

dT

dT

dy

(*2 — *1) + ІУ-1 — j/i) . (xt — JCj)» ’

1 +Га ’

dS

dxі = dxj cos at — *1 sin ai — dy sin ai — cos ai; dyi — dx I sin ai 4- x{ cos ai 4- dy cos aj — y[ sin ай d$ =

JQ d(SC)-(SK)~d(SK)-(SC) .

{SKV ’

К 1 — 52

d(SK) = 2(;cia2dx:i 4* уФ2 dy) d(SC) =a(b’dyl + SQdxi 4- ;

SQ = ]/"a2*2 4- b2y2 — a2fr2,

где SC, SK — числитель и знаменатель выражения (7.40).

Выражения (7.43), полученные для таких кинематиче­ских параметров, как угловая скорость и ускорение вра­щения кривошипа, зависящие от линейной скорости дви­жения цепи и параметров эллиптического делительного контура ведущей звездочки, позволяют перейти к анализу эффективности передачи.

Современный привод велосипеда характеризуется ком­бинацией трехзвенной биомеханической СНКГ и механи­ческой педально-кривошипной цепной системы. Если ки­нематические параметры механической части общей си­стемы привода — вполне определенные и стабильные, то

параметры биомеханической части этой системы являются переменными в пределах одного цикла педалирования.

Последнее обстоятельство позволяет выделить два важ­ных для процесса педалирования аспекта. Первый — су­губо биомеханический, т. е. связанный с эффективностью использования мышечной работы в различных фазах и положениях СНКГ, определяемых углом поворота кри­вошипа. Второй — сугубо механический, т. е. связанный с рационализацией кинетостатики СНКГ. Биомеханиче­ский аспект педалирования индивидуален для каждого гонщика и весьма сложен для анализа из-за отсутствия необходимого объема достоверной информации, на осно­вании которой можно было бы построить и рассчитать био­механические модели. Некоторые сведения из этой области исследований изложены в гл. 2 и п. 7.2. В настоящем параграфе рассматривается только механический аспект, что позволяет ответить на вопрос: можно ли совершенство­вать механизм привода велосипеда с целью уменьшения энергозатрат на организацию его движения? Но, с другой стороны, не приведет ли применение эллиптических веду­щих звездочек в приводе к дополнительным затратам энергии гонщика? Другими словами, можно ли оптими­зировать параметры привода велосипеда для конкретного гонщика с учетом особенностей СНКГ?

В механическом аспекте СНКГ можно представить (см. рис. 7.13, а) в виде коромысла /3 (бедро) и шатуна /2 (система голень—стопа) совместно с кривошипом вело­сипеда, образующих плоский сдвоенный кривошипно­шатунный механизм с переменным параметром /2. Вектор­ный контур механизма позволяет записать векторное

уравнение:

f=5

£ U = h + h — Із — yot — X0, = 0. (7.44)

i

Проекции векторов на оси координат xOLy:

ха + h cos а2 — Із cos а3 — х0. = 0; ")

… . . „ f (7.45)

у а + ‘2 sin а2 — Н sin а3 — y0i = 0, J

где

хА = /і cos «j; уА = 1г sin at.

Введем передаточную функцию vA/a>L = dx^da^. Обо­значив dxA/dai — Рха и d2XA/da = РРха и выполнив

дифференцирование уравнений (7.45) по аргументу а1( получим выражения

РРхА — /2 cos а2 • Ра2 — /2 sin а2 • РРа2 —

— РІ2 sin а2 • Ра2 + /3 cos аз • Pal — j — Із sin аз • РРаз = 0;

РРг/л — /2 sin а2 • Раї — j — /2 cos а2 • РРа2 +

+ РІ2 cos аг • Ра2 -!- Із sin а3 • Раз — /3 cos а3 • РРа3 = 0.

(7.46)

СНКГ обладает весьма значительной распределенной массой. Так, при массе гонщика 72 кг общая масса СНКГ составляет (см. рис. 2.12) 27,4 кг. Отдельные элементы СНКГ движутся с большими скоростями и ускорениями, что приводит к большим инерционным нагрузкам, поэтому преодоление сопротивления инерции требует от гонщика дополнительных энергозатрат. Эти энергозатраты могут быть использованы для оценки эффективности привода в системе гонщик—велосипед.

Для рассматриваемой схемы механизма привода (см. рис. 7.13, а) введены следующие обозначения: 5г — ЦМ сбалансированной кривошипно-педальной системы; S2 — приведенный ЦМ системы голень—стопа; S3 — ЦМ бедра. Аналогично приведенным выше зависимостям получим следующие уравнения:

для ЦМ звена /2:

*s2 = ха + AS2 cos а2; PxSi = рхА — ^S2 sin а2-Ра2;

ys2 = У а + ЛЗг sin а2; Pys2 = рУл + A S2 cos а2-Ра2;

PPxs2 = РРха — ^S2 cos а2-Ра2 — /4S2 sin а2-РРа2;

PPys2 = РРул — AS2 sin a2 • Pal + AS2 cos a2 • PPa2;

для ЦМ звена /.,: xss = xA — j — O1S3 cos a3; PxSa = PxA — O1S3 sin a3-Pa3;

ys, = У a + O1S3 sin a3; Pys, = Рул + O1S3 cos а3-Ра3

PPxSs = PPxa — OiS3Cosa3-Pa3 — OiS3sin аз-РРа3;

PPys, = PPya — OiSssin аз-Раз — j — 0[S3cosa3-PPa3.

Центр масс Si сдвоенного звена Ul лежит на оси шар­нира О.

Дальнейший кинетостатический анализ действующих сит можно выполнить согласно методике, изложенной’

в п. 7.3, в соответствии с рис. 7,14. В результате получим выражения для сил инерции Ft и моментов инерции

F2 = —М2 • PPxs2 • w ь Fy2 = ~M2-PPySs-cof; (7.47)

Fx3 = ~M3-PPySs. af, F$ = — M3-PPySa-a2u (7.48)

где

Ліг = —J2-PPa2-М3 — ■—Jz-РРаз-ш].

Из рассмотрения двухзвенной группы АВ01 на осно­вании уравнений моментов и сил

£ М (В)2 = 0; £ М (В)3 = 0; £ F* = 0; £ F? = 0

(7.4 У)

определяются реакции в шарнирах и, в частности, в шар­нире А (см. рис. 7.14):

(7.50)

Rl—1 — ТI_2COS <Х2 — Л^1—2 Sin СЖ2 = —/?2—ii

Ri-2 = 7’i_2sina2 + Ni_2cos a2 = — Rl_t.

Из рассмотрения кривошипа АО на основании урав­нений моментов и сил

£М(0) = 0; SFf = 0; £ Ff = 0 (7.51)

определяются составляющие Rо_і и Ro-i реакции в шар. нире О, а также движущая сила Q и движущий момент М.

Расчет рассматриваемой системы был выполнен для условного гонщика, обладающего следующими антропометрическими данными: масса 72 кг; длина бедра Л2 = 0,433 м; длина голени А3 — 0,448 м; длина стопы А4 = 0,147 м (см. рис. 2.7).

Параметры цепного привода (длина кривошипа 1г = 0,170 м, со­отношение звездочек г, X г, = 51 X 14 и частота педалирования / = = 107 об/мин) соответствуют результату в часовой индивидуальной гонке на треке около 50 км (точно 50,371 км).

На примере кинограммы педалирования Ж- Анкетиля составлена таблица параметров /2 и 1’2, которые идентичны друг другу и сдвинуты по фазе на угол я (табл. 7.8). Угола, = 0 (см. рис. 7.13, а) соответствует вертикальному верхнему положению кривошипа 1. Таблица построена для восьми положений кривошипа. При расчетах это число принималось равным 16. Угол ф между кривошипом и малой осью эллипса варьиро­вался в интервале 0 ^ ф ^ я. Малая полуось эллипса изменялась в пределах 0,5/0 ^ b г0.

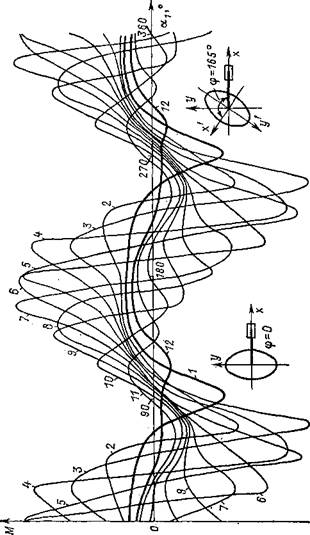
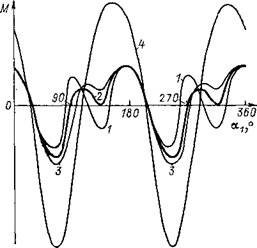
Расчеты показали, что в цепном приводе с эллиптической ведущей звездочкой энергозатраты на преодоление инерционного сопротивле­ния СНКГ существенно зависят от параметров эллипса (рис. 7.17). Кривая 1 характеризует привод с круглой ведущей звездочкой, когда а = Ь = 0,08246. Часть кривой, расположенная выше оси абсцисс, ха-

Таблица 7.8. Параметры 12 и 1’2 замещающего механизма в соответствии с кинограммой Ж. Анкетиля а». ° h h а„ ° 1% и м М 0 0,598 0,572 180 0,572 0,598 45 0,588 0,586 225 0,586 0,588 90 0,572 0,600 270 0,600 0,572 135 0,566 0,604 315 0,604 0,566

А о Рис. 7.17. Крутящий момент М привода СНКГ в функции от угла поворота кривошипа оц для ряда соотношений параметров эллипса ведущей звездочки цепного привода:

Кривая	а. м	Ь, м
1	0,8 0246	0,08246
2	0,07215	0,09277
3	0,09277	0,07215
4	0,11339	0,05154
5	0,05154	0,11339

рактеризует момент, необходимый для привода СНКГ, часть кривой, расположенная ниже оси абсцисс, — момент, возникающий в резуль* тате действия сил инерции и способствующий движению СНКГ.

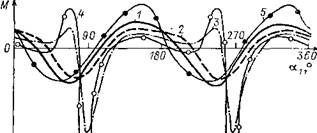
Наиболее эффективным из рассмотренных вариантов, т. е. обеспе­чивающим минимальную работу в цикле педалирования для привода СНКГ, является привод с эллиптической ведущей звездочкой с пара­метрами а = 0,07215 ми b — 0,09277 м (кривая 2). Последующие рас­четы в целях оптимизации угла ф (угла сдвига осей эллипса относитель­но кривошипа) показали, что из рассмотренных вариантов наиболее эффективным является угол ф= 165° (рис. 7.18). Последующее уточ­нение этого параметра дало результат ф = 155° и соответственно b! r0 = = 0,82, откуда Ъ = 0,08450 м. На рис. 7.19 приведены графики оптими-

зации параметров пригода с эллиптической ведущей звездочкой. Из рисунка видно, что процесс педалирования является оптимальным по параметру (работа, затраченная в одном цикле педалирования) при Ь = 0,0804 м (кривая 1). Рис. 7.19. Графики оптимизации параметра о эл­липса ведущей звездочки привода СНКГ при ф = = 155°. Значения Ь, м: t ■*. 0,08040; 2 — 0,08450; 3 — 0,08660: 4 — 0,10303