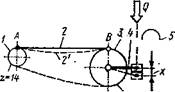
Динамика системы гонщик — велосипед

Кинетостати чески й анализ, например выполнен­ный в п. 8.2, проводится без учета упругих свойств звень­ев и, как правило, приводит к результатам, не в полной мере соответствующим наблюдаемым в действительности. Поэтому практический интерес представляет изучение влияния упругих свойств отдельных элементов и всей системы гонщик — велосипед на ее динамические харак­теристики.

Из всего многообразия возможных динамических моде­лей рассмотрим модель привода, учитывающую упругие свойства основных его звеньев. При этом ограничимся только изучением влияния крутильных и изгибных дефор­маций, а также деформаций растяжения элементов при­вода.

Для такой динамической модели введем обозначения: J о, &01 — момент инерции периферийной части одно — трубки, соприкасающейся с дорожным покрытием, и ее приведенная крутильная жесткость; Jlt k12 — суммарный момент инерции однотрубки, обода и спицевого набора и их приведенная крутильная жесткость; /2 — момент инерции втулки колеса и системы ведомых звездочек; k23 — крутильная жесткость цепной передачи; П (ср3) — функция положения цепной передачи; — момент инер­ции системы ведущих звездочек, кривошипов, педалей и части нижних конечностей гонщика; Мд—движущий момент; ф0, фь ф2, Фз — угловые координаты вращения элементов модели вокруг своих осей.

На основании уравнений Лагранжа второго рода, кинетической и потенциальной энергий рассматриваемой

системы получены уравнения движения:

JоФо + *м (Фо — Фі) = —РоГо>

(8.39)

Лфі — *оі (фо — Фі) + *12 (Фі — фг) = O’.

«/2Ф2 — *12 (фі Фг) "f" *23 I Фг П (фз)] =

*^зфз *гз [фг П (ф3)] П (ф3) = УИд.

Величины F0 — Fx и г0 = гх соответствуют величинам, найденным при кинетостатических исследованиях. Учи­тывая это, а также пренебрегая величиной J0 вследствие ее малости, систему (8.39) можно записать в упрощенной форме:

(8.40)

Лфі + *12 (Фі — Фг) = —Firii Л Фг — *12 (фі — Фг) + *23 1фг — П (Фа)] = 0; Лфз-*2з[ф2-/7(фз)]/Г(фз) = Мд.

В системе уравнений (8.40) Fx = f„N1, где Nj опре­деляется равенством. (8.16). Рассматривая упрощенный вариант движения велосипеда по горизонтальному участ­ку (а = 0) и случай одинаковых колес (у = 0), а также полагая, что Sy = 0, найдем

(8.41)

F — Г (та-1 АіЯі ~A*g + SxyS •і — /к {tn0g Н

где

Ai = гх (тг + т2) + msy3;

А2 = m2L + тях3 — fKm0.

В равенстве (8.41) хг = ггфг и, следовательно, урав­нения (8.40) запишутся в виде:

Л

^1) Фі "f* *12 (Фі Фг) —

/к’і

—fKritn0g + -х5- (A2g — Sxy3y,

Лф2 — *12 (Фі — Фг) + *2s Іфг — П (ф8)] = 0;

Лфз — *2з (Фг — П (Фа)1 Я’ (ф3) = Мд.

Обозначим закон угловых перемещений кривошипа через фз (0, тогда получим

фз = Фз (/) + ?з (/), (8.43)

где <7з (t) ‘— малые отклонения колебательного типа.

(8.42)

Используя уравнение (8.43), произведем линеаризацию функции положения цепной передачи П (ф3) и ее произ­водной П’ (фз):

П (фз) = П (фз -}- « П (фз) -{- П (фз) qs )

П (фз) = П (фз — J — <?з) л* П (фз) + П (фз) 9з — J ^ ^

Функции фі(<) и ф2 (t) также представили как сумму их координат фГ (/) и ф5 (/) и соответствующих откло­нений ft (I) и q2 (0:

Фі (0 = ФЇ (0 + q (О = П (фз) + q\ j

Ф2 (t) = Ф2 (t) + q2 (0 = П (ф|) + q2. J {S-45)

В первом приближении силу сопротивления набегаю­щего воздушного потока Sx [см. выражение (8.41)] можно считать постоянной и соответствующей средней скорости движения л:ср = фзiru где і = П’ср (фз) — передаточное отношение цепного привода. Тогда правая часть первого уравнения системы (8.42) тоже будет постоянной и рав­ной А3:

Аз = —f«ritn0g + (A2g — S^a).

Движущий момент Мд будем считать функцией частоты вращения кривошипа ра:

МА = Mo + АМ cos фз (t). (8.46)

В результате система уравнений (8.42) преобразуется к виду:

Jq + &12 (q — Qi) = Аг — J [П’ (фз) фз2 + ГІ (фз) фз];

— ki2 (qi — q2) + &23 [q2 — П (фз) <?з] —

= —J2 .П (фз)фз2-Ь^ (фз) фз]*

Jzqz — &гз[q2 — П (фз)^з]/7 (фз)=^1о + АМсоЗфз(t)—Дфз,

(8.47)

где

JlSSJ1 + J^LAl.

Кроме того, в системе уравнений (8.47) опущены сла­гаемые второго порядка малости относительно величин <7г и 93-

Решение системы линейных, неоднородных, с перемен­ными коэффициентами уравнений найдем с помощью ме­тода разложения по формам собственных колебаний, для

чего рассмотрим систему с нулевыми правыми частями и определим переменные собственные частоты ojj и неста­ционарные коэффициенты форм колебаний а^ (J — I, 2, 3). Решение однородной системы (8.47) соответствую­щее частоте мг, будем искать в виде

qj = ajr (т) cos Фг (т), (8.48)

где т — параметр, соответствующий времени, причем Фг (т) = на, (т).

При этих условиях из уравнения (8.48) можно полу­чить

<7/ =—а/,®, собФл. (8.49)

Для существования отличных от нуля значений а}т необходимо выполнить равенство

Д(0 =

k2 — J j СО J (/) k2 О

—&12 &12-f-&23—Л®?(0 —&23^7′(фз) =0.

0 —&2з/7 (фз) &23П (фз) — J3®г (0

(8.50)

Раскрыв частотный определитель, получим алгебраи­ческое уравнение третьей степени относительно <з>1 (/), из которого могут быть найдены три группы значений собственных частот: Шц (/), со2 (І) и ю3 (t), причем м, (ґ) = = 0. Отметим, что при П’ (q>Ј) = const = і из системы уравнений (8.50) определяются три действительных зна­чения собственных частот «а^, а>г и щ.

Для нахождения коэффициентов форм собственных колебаний положим а^г — 1 и решим следующую систему уравнений:

(8.51)

ki2 — Jitot(t) — kl2a2r = 0; )

—&23Я’ (фз) а2г + [*2зП’‘ (фз) — Уз©? (01 азг = 0. j

Преобразуя систему уравнений (8.51), найдем:

«гг = 1 (/•= 1, 2, 3);

kt а

а«г =*

(8.52)

kl2~jyr(t) ^12^2д/7 (ф* )

^ [*12 ~ (О] [*2зЛ" (Фз*) ~ М]

«Яг =

Из системы уравнений (8.52) видно, что коэффициенты форм собственных колебаний а}1 переменны, так как они зависят от значений П’ (<pj) и to, (t).

В этом случае решение системы уравнений (8.52) будем искать в виде

/•=3 <7; = Е airTr-

Г=

После соответствующих подстановок найдем:

г=3 г=3

«Л Е а1 гТг “Ь *12 Е (® 1Г а2г) Tr — fi (t)

r= 1 r=1

г—3 З

./2 Е 0C2rTг *12 Е (®tr ®2г) Tг -}-

г=1 г=1

г=3 + *23 Е |а2г— П’ (фз)азліТ’г = /г (0;

г=1

г=3 г=3

Уз Е азгТг — *23/7′ (фз) Е 1«2г — /7′ (фз)а3г] 7V = /3(0-

Г=1 Г=1

(8.53)

Из условия ортогональности форм собственных коле­баний следует, что при s=Ј= г, где s, г — номера форм колебаний, получим

/=з

Е JjO-js^ir — 0- (8.54)

/=і

На основании уравнений (8.53) с учетом (8.54) имеем

Т, + «>г (о тг = h (-l+ h (і-]-а;гг + Ш **. = Fr (8>55)

J, -(- J2a2r + J3a3r

где /і (t), /2 (t)> /з (0 — правые части системы уравне­ний (8.53).

Рассмотрим реализацию уравнения (8.55) на основе приближенных методов решения. Если выполняется ус­ловие

« 1.

0.5 -%7тт— 0,75 “г(0

о>|! (О ’ сор (t)

то удобно воспользоваться приближенным методом, в соот­ветствии с которым частные решения уравнения

7 + о)|(0Г, = 0 (8.56)

записываются в виде:

Уп = V "^ПТГ Sln I ®г ^ dt;

(8.57)

О

_________ I

Уг2 = V~^TWcos ICOr wdL

Общее решение однородного уравнения (8.56) пред­ставляется в следующей форме:

Т т, о = СіУп ~Ь С2уГ2- (8.58)

На основе частных решений (8.57) общее решение не­однородного уравнения (8.55) может быть построено по­средством метода вариации производных и постоянных:

t t

тг = — Уп J 1wr dt + У™ I Jwr dt + СхУп + С‘іУгі’ (8-59)

о r о

где

Wr = yrJyr2 — ynyn = —wr (0) = const.

Определив функцию Tr и воспользовавшись соотноше­ниями (8.52), (8.45) и (8.43), найдем:

г=3

ф/ = ф/ “Ь S &irTг

г= 1 г=3

X, = Г і Х = п Х = Г

ф* + S тг

(8.60)

г= 1

г-= 3

фГ + S тг

Г=1

фГ + 5 Тг

г=1

Три последних уравнения (8.60) определяют переме­щения, скорость и ускорения системы гонщик — велоси­пед в поступательном движении.

Анализ рассмотренной динамической модели показы­вает, что данная задача достаточно сложна и не допускает решения в конечном общем виде. Поэтому для исследова­ния кинематики динамической модели необходимо ввести в уравнения движения конкретные значения всех пара­метров в виде функций П (фй), П’ (фз).

Рассмотрим динамическую задачу в несколько упро­щенной постановке, считая, что П’ (фз) = і = const. Предварительно установим закон изменения фз (і), для чего приведем все моменты инерции и внешние силы к оси ведущей звездочки:

Упр = (Jt — J- У2) Iі — j" Ja< М = Лі 4- Мп.

Тогда уравнение движения ведущей звездочки запи­шется в виде

Упрфз = Мд + Аі = Мо + ДМсо5фз*а) + ^і. (8.61)

Для того чтобы движение системы было установив­шимся, необходимо выполнение равенства М0 + А і = 0. В противном случае будет происходить или ускорение системы (при Мо + /4і>0), или ее торможение (при М0 + Ai < 0). В итоге получим нелинейное дифферен­циальное уравнение

Фз т^- cos фз = 0. (8.62)

•’ Пр

Для решения уравнения (8.62) примем фз = prf — f — + Дфз, где рз — средняя частота вращения кривошипа; Дфз — малые периодические отклонения угловых пере­мещений фз в функции p3t. С учетом принятых допущений получим

COS фз = cos (pzt — f — Дфз) л; cos p3t — Дфз sin p3t. (8.63)

После подстановки найденного значения cos фз в урав­нение (8.62) получим:

фз + 4^“ АФз sin р£ = -4^- cos pzt. (8.64)

J пр J пр

Для решения уравнения (8.64) воспользуемся методом гармонического баланса, причем при поиске периодиче­ского решения ограничимся двумя первыми гармони­ками, т. е.

Дф3 А0 + Ах cos p3t + sin p3t +

+ А2 cos 2 p3t + Вг sin 2pst. (8.65)

После соответствующих подстановок получим л, 8J р|дл* , — ,

Афз Ю^-ДМ2 C0Spat 16Уцр/?з — ДМ2 Sln М

(8.66)

Так как значение Дфз определялось из кинетостати — ческих представлений, то следует сделать вывод, что даже без учета упругих свойств привода возможны колебания кинематических характеристик с высшими гармониками.

Обозначим коэффициенты уравнения (8.66) через At и В.2. При постоянных параметрах системы Mr (/) = = ©г (0) частные решения (8.57) представляются в вид<? уп = sin «)Tt и у гг = cos wrt. С учетом постоянства IV (фз*) зависимости (t), /2 (t) и f3 (/) будут иметь вид.

/і (0 = А + hi (Лірі cos рз^ + В-г^рІ sin 2 рзі)’, h (0 = hi (А і pi cos pzt — f Вчръ sin 2pzt) f3 (t) = M0 — f Д M [cos p3t — (/їх cos p4 +

+ B2 sin 2p:.t) sin pzt] — f h{Ap cos pd + В24рз sin 2p3t).

(8.67)

При полученных выражениях для возмущающих фак­торов интегралы, входящие в уравнение (8.59), могут быть найдены в конечном виде и функции времени Опи­шутся следующим уравнением:

rp Р у lSfl)r. Л.

T’ = —Qir~ «» —

,, cos + С, sin и, і + С, cos м, і, (8.68)

Q («О, — 9Рд)

где

Р = А + М0а3г;

Q — ®г (it У2&2г “Ь УзОСЗг)»

7? = ^41(«/1 — f — IzCdr) + (ДМ + IzAf? z —ДМВ^ а^;

5 = 4В2рз ( Ji + І2І&2Г + Ізазг —r ДМ Л іазг) ;

М = — j &МВ2.

Поскольку входящие в уравнение (8.68) величины известны, задачу определения параметров движения си­стемы гонщик — велосипед с учетом упругих свойств привода можно считать решенной. Из уравнения видно, что колебательный процесс имеет составляющие с соб­ственными частотами юг и три гармоники от внешнего возмущения со средней частотой р3. Для устойчивой

307

работы привода необходимо обеспечить выполнение усло­вия, определяющего возможные значения низшей соб* ственной частоты колебаний «>!, т. е. 3ра.

Необходимо отметить, что основным фактором, ВЛИЯЮ­ЩИМ на амплитудные значения функции Тг, а следова­тельно, и на интенсивность колебательных процессов, является величина АМ переменной части движущего момента. Так, при AM = 0 величины R, S и М равны нулю и колебания с частотой р3 или с частотами, крат­ными ей, отсутствуют. Остаются только колебания с соб­ственной частотой, которые могут возбуждаться только

Ічі/ ного определения Г.,———————————

сткости цепного привода гоночного велосипеда

случайными причинами, но, как известно, эти колебания достаточно быстро затухают и при установившемся дви­жении их можно не учитывать.

При проектировании и сравнительной оценке конструк­ции гоночных велосипедов и их приводных систем важ­нейшими характеристиками являются частотный спектр и чувствительность собственных частот к изменению пара­метров отдельных элементов системы, в частности при­водной передачи. Проанализируем степень влияния жест­костей k12 (крутильной жесткости заднего ведущего ко­леса) и ka (приведенной крутильной жесткости цепного привода) на значения собственных частот ю2 и са3 при со. = 0.

Исходные значения параметров, необходимых для расчета, были определены экспериментально на стандарт­ном цепном приводе. Так, жесткостные характеристики спицевого набора и однотрубок были определены согласно схеме измерений на рис. 6.6. Жесткостные характери­стики цепного привода были определены согласно схеме на рис. 8.35. Для этого ведомую звездочку 1 жестко фик­сировали в специальном приспособлении. Цепь 2 имела возможность свободного провисания (положение 2′) в меру общего натяжения цепи при настройке системы привода. Ведущее колесо 3 при приложении к педали 4 усилия Q разворачивалось по часовой стрелке. Приведенная дефор-

S) ai, с 1000 800 600 400 200

0,5 1

1,5 ? 2 Ьі-10,НІм

1200 800 400

0

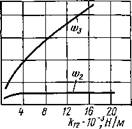
0 Рис. 8.36. Графики изменения собственных частот системы привода гоночного велосипеда в функции жесткостей 0,16;; < ktJ <; 10 kij, ГДЄ Через kij обозначены ИХ HO- минальные значения. Моменты инерции элементов рас- считываемой модели были приняты: Jx — 0,72 кг-м2; У2 = 7.10"3 кгм2; У3 = 60’Ю-3 кг-м2; П (<р3) = г21 = zjz2 = 48/14 = 3,43. На рис. 8.36, а показаны рассчитанные зависимости ю2 и ю3 от kn. Как видно, изменение жесткости к1г от 177 до 17 700 Н/м вызывает увеличение собственной ча- стоты со2 только в начале диапазона, а затем, начиная с kl2 = 1500 Н/м, происходит «насыщение» и величина со2 асимптотически стремится к значению со2 = 200 с-1. Это свидетельствует о том, что существующие значения жест- кости k12 достаточны и, например, применение более жестких по параметрам крутильной жесткости дисковых колес не увеличивает значение собственной частоты ю.2. В то же время очевидно сильное влияние величины kl2 на значение высшей собственной частоты ю3. Последняя, однако, мало влияет на динамическую характеристику привода велосипеда. На рис. 8.36, б дана аналогичная зависимость частот со2 и % от жесткости /г23, изменяющейся в диапазоне 20—

мация х фиксировалась индикатором 5. В проведенном эксперименте приведенная жесткость k2S складывалась из продольной жесткости цепи (см. рис. 6.26), жесткости провисающей цепи на участке АВ (см. рис. 6.30 и 6.31), из- гибной и крутильной жесткости кривошипа и изгиб- ной жесткости оси педали. Номинальные значения экспериментально определен- ных жесткостей: kX2 = 1770 Н/м; ki3 = 202 Н/м. Изме- нение каждой из жесткостей рассматривалось в диапазоне а)ш, с то

2020 Н/м. Из графиков видно, что значения собственной частоты (о2 более чувствительны к изменению жесткости &23, чем значения (о3. Вместе с тем изменение жесткости t23 вблизи ее номинальных значений не позволяет сущест­венно изменить низшую собственную частоту.

В связи с изложенным при необходимости увеличения низшей собственной частоты со2 целесообразно одновре­менное увеличение жесткостей kn и /г23. Так, при увеличе­нии каждой из них в 1,5 раза по сравнению с номиналь­ными значениями собственные частоты становятся рав­ными: ©2 = 230 с"1; м3 = 660 с’1.

[1] В технической и методической литературе по велоспорту, а также в обиходе укоренился и постоянно используется неправильный с тех­нической точки зрения термин «шатун». В настоящей книге эта деталь велосипеда будет именоваться кривошипом.

[2] ei max (а2)а,=о | = єі (-7-) = —■ sin (я/2г2); (6.45)

*2 / oti=u Zj

I ®1 min (^2)а,=0 I = 0. (6.46)

Уравнение (6.45) соответствует асинфазному режиму, Уравнение (6.46) — синфазному.

[4] Примером может служить попытка выполнить поворот на скольз­кой обледенелой дороге, когда разворот колеса не изменяет траекторию движения, а приводит только к падению из-за потери устойчивости.

[5]1 max — g (/max COS CL Sin Ot).